14. Die Dreiecksseite AA-AB

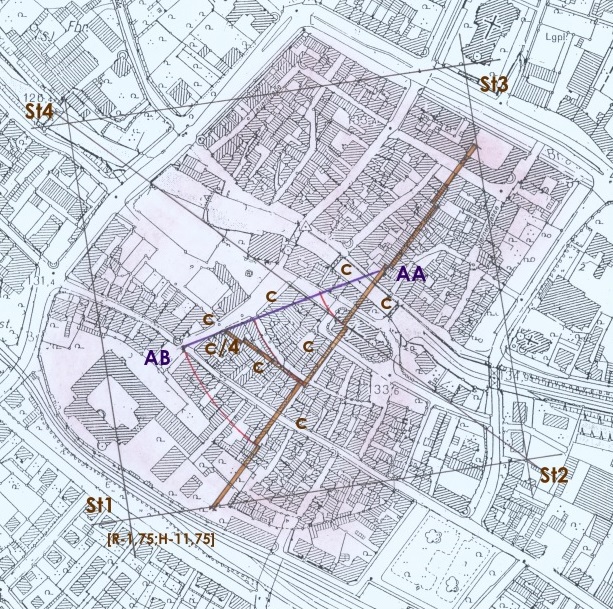
Abb. 17 Eine Katasterkarte der Altstadt mit dem Steinkreuzviertel­quadrat St1-St2-St3-St4, der Parallelen zur Diagonalen und der Dreiecks­seite AB-AA.

Die Lage von Punkt AA ist festgelegt mit Hilfe einfa­cher Grundelemente des Steinkreuzviertelquadrates. Der Punkt bleibt mit dem Steinkreuznetz fest verbun­den. Die Länge der hier konstruierten Dreiecksseite AA-AB ist gleich 3c, das heißt mit 3/6 halb so lang wie die Paral­lele zur Stein­kreuzdiagonalen (vgl. Abb. 16). Zur Bestimmung des Win­kels, mit dem die Dreiecks­seite von der Richtung Stein­kreuzdiagonalen abweichen sollte, entschied man sich für das Verhältnis 5 zu 8 aus der Zahlenreihe 3‑5‑8‑13 usw. zum Goldenen Schnitt, 8 Einheiten auf der Parallelen in Steinkreuz-Diagonal­rich­tung, 5 Einheiten senkrecht dazu (vgl. Abb. 24). Der Winkel, der dabei entsteht, kommt im Dreieck selbst nicht vor. Die Dreiecksgeometrie, die sich aus dem Winkelverhältnis 1 zu Wurzel 2  entwickelt, dreht das Dreieck um den Punkt AA in eine eigene Richtung (vgl. Abb. 25).

Das später angelegte Grundrechteck der erweiterten Stadt entstand mit einer ganz anderen Geometrie, aber nach dem gleichen Muster: Um einen Festpunkt im Steinkreuznetz, dort Punkt C, wird eine einfache geometrische Figur gedreht, die ihre Maße und ihre Gliederung aus dem Steinkreuznetz mitbringt (vgl. Abb. 11ff.). Bei gleicher Drehrichtung ist auch das Win­kel­maß in beiden Fällen fast gleich.

→ WEITERLESEN