A powerful architecture & Construction theme.
Construct your website in the perfect Ratio.
Alienum phaedrum torquatos nec eu, vis detraxit periculis ex, nihil expetendis in mei. Mei an pericula
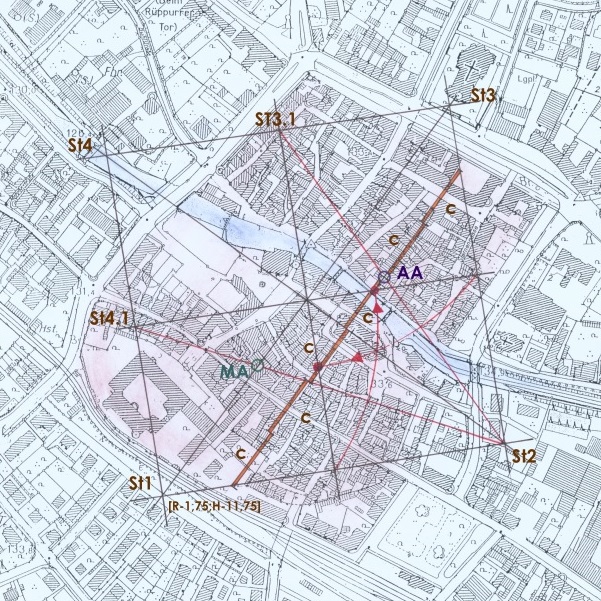
Abb. 16 Eine Katasterkarte der Altstadt mit dem Steinkreuzviertelquadrat St1-St2-St3-St4 und der Parallelen zur Diagonalen St1-St3.
In das Steinkreuzviertelquadrat St1-St2-St3-St4 ist eine Parallele zur Diagonalen St1-St3 eingemessen. Das Abstandsmaß ist das Ergebnis einer geometrischen Konstruktion, die mit der Längendifferenz von Quadratseite und halber Diagonalen operiert: Zwei Kreisbögen um St3.1 und St4.1, mit den Diagonalen der kleinen Quadrate als Radien, schneiden die mittleren Teilungslinien des Steinkreuzquadrates in P1 und P2 (Abb. 23). Die Parallele läuft durch diese zwei Punkte.
Die Halbdiagonalen von Punkt St2 zu den Mittelpunkten der gegenüberliegenden Seiten St3.1 und St4.1 teilen die Diagonale St1-St3 und die Parallele in jeweils drei gleiche Abschnitte. Punkt AA ist ein Teilpunkt. Die drei Abschnitte werden halbiert. Es entsteht das Maß „c“ (vgl. Abb. 23).
Eine auffallend gerade Reihe von Grenzsteinen auf dieser Linie beginnt nördlich der Albstraße.
In einer Rekonstruktionszeichnung der Vorgängerkirche von St. Martin aus dem 14. Jahrhundert * liegt deren Westfassade auf der Parallelen.
Punk AA auf der Parallelen ist die Spitze des Alten Dreiecks.
Punkt MA auf der Diagonalen ist der Mittelpunkt des bereits erwähnten Kreises (Abb. 4), der für die Zuordnung der drei Türme der Stadt zuständig ist.
Ettlingen, Geometrie