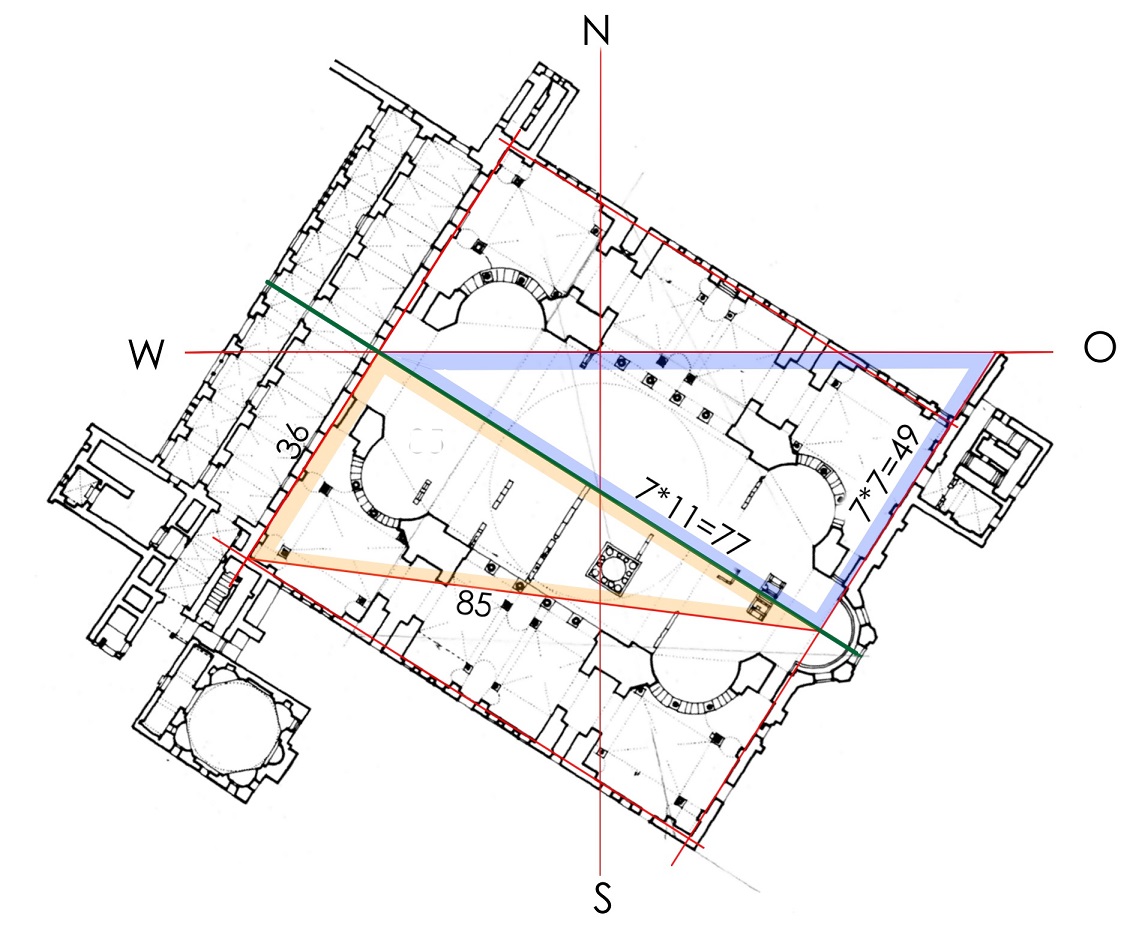
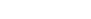14. Istanbul, Hagia Sophia
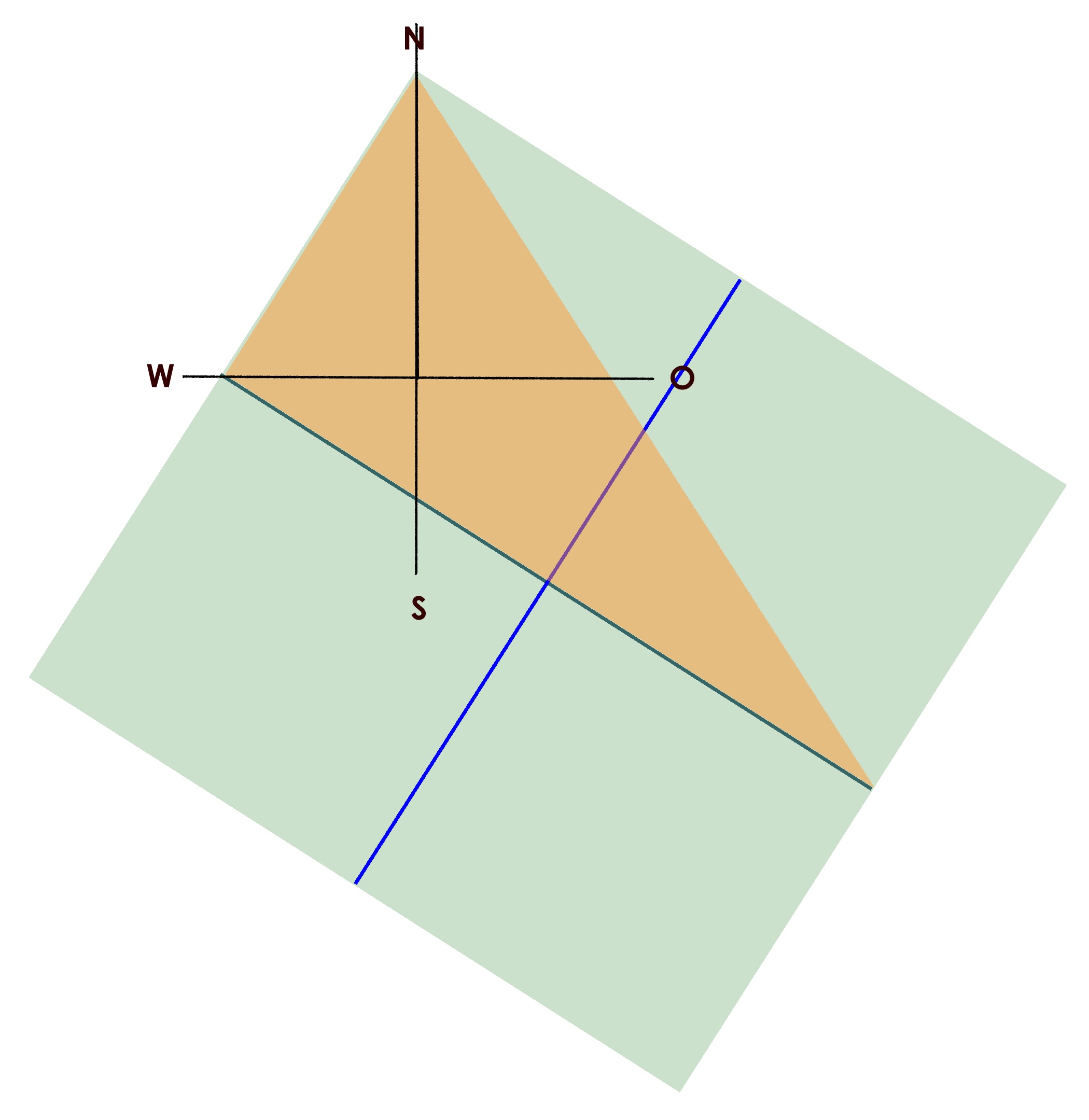
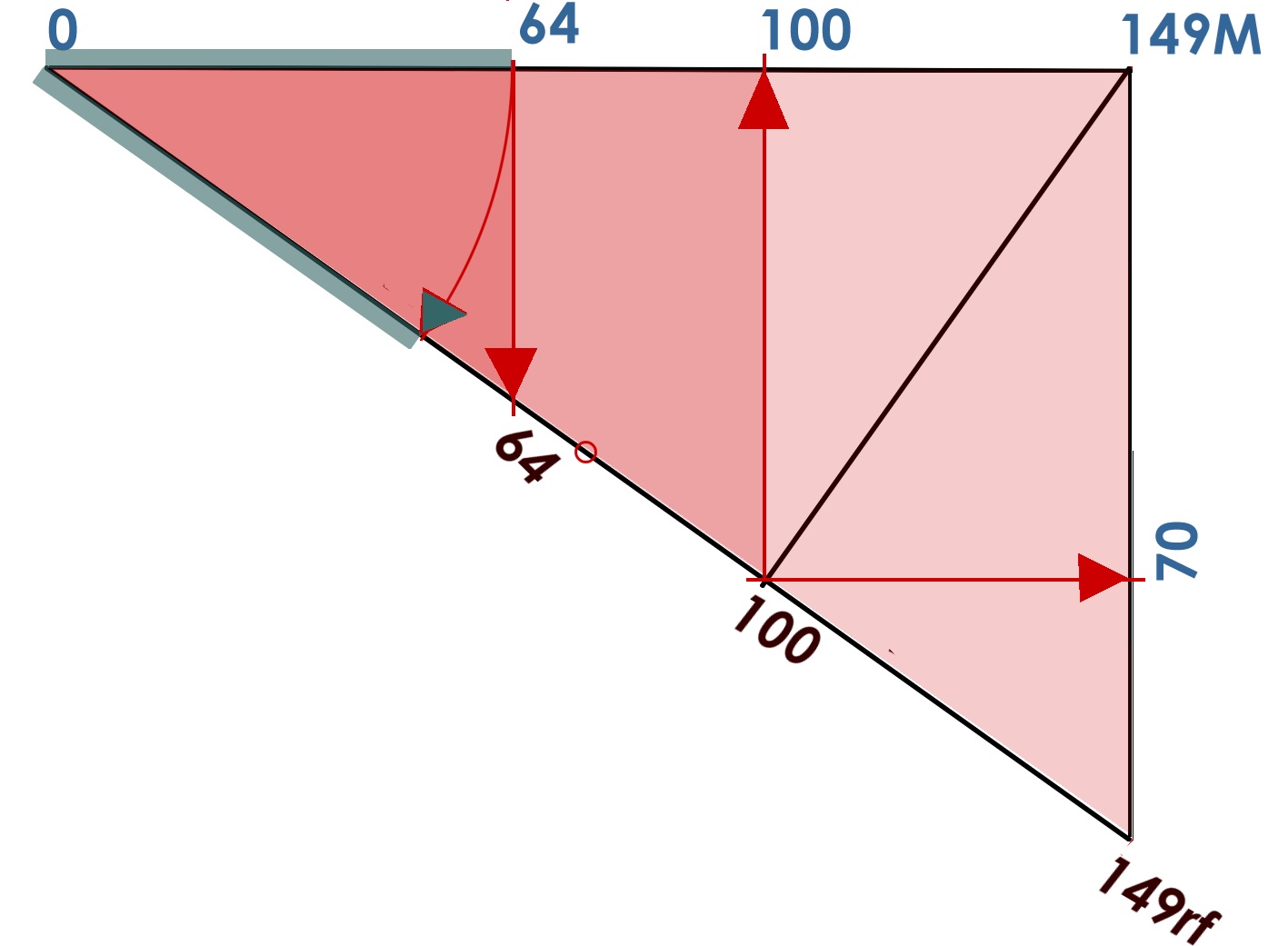
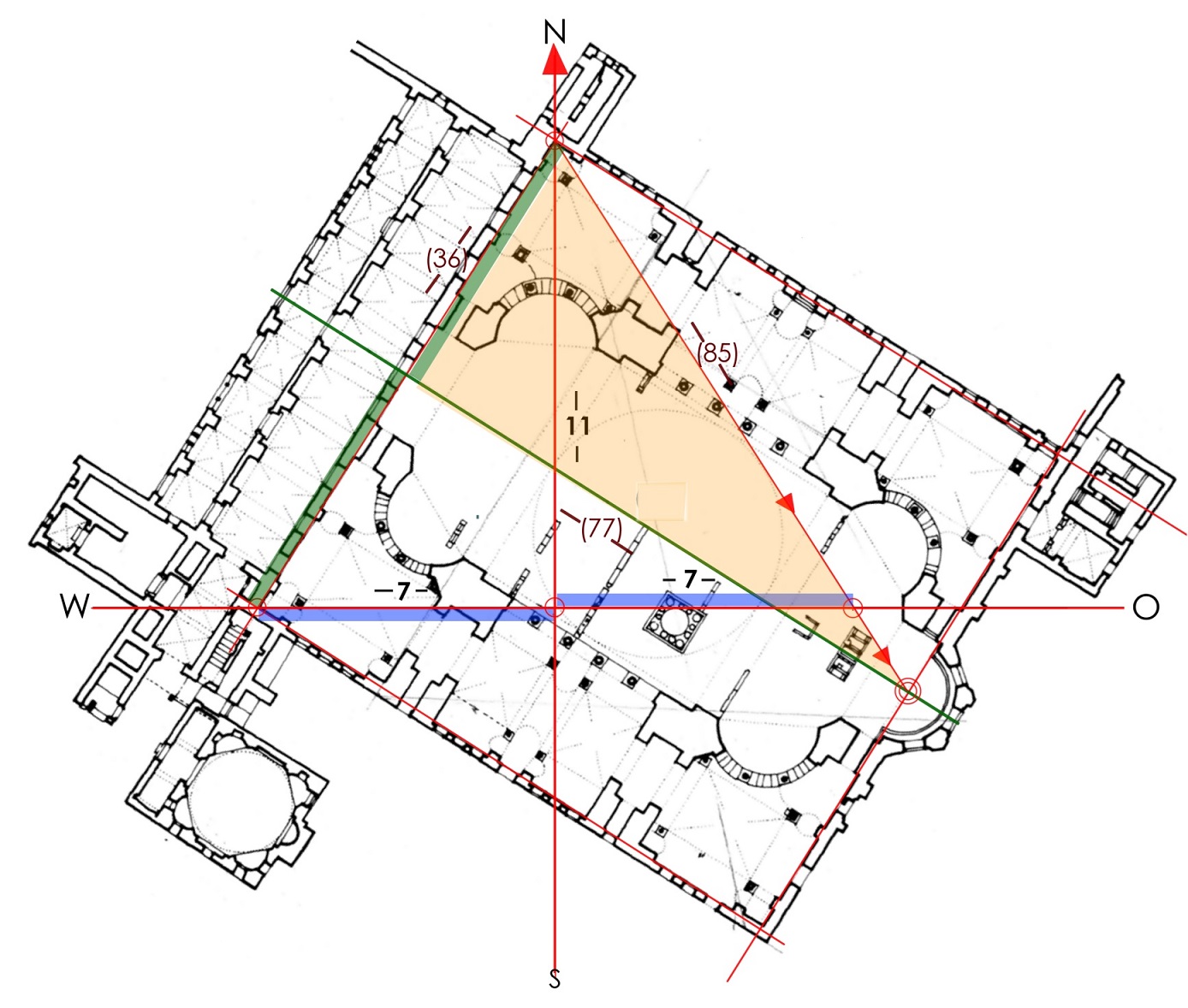
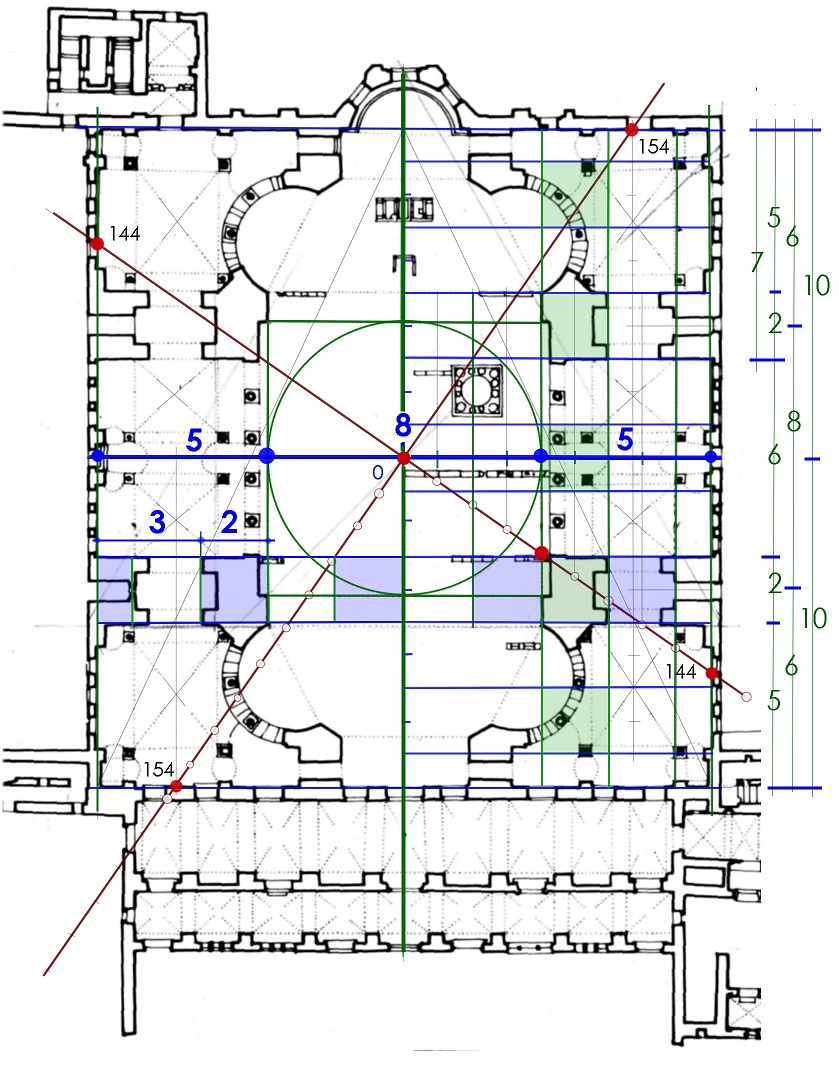
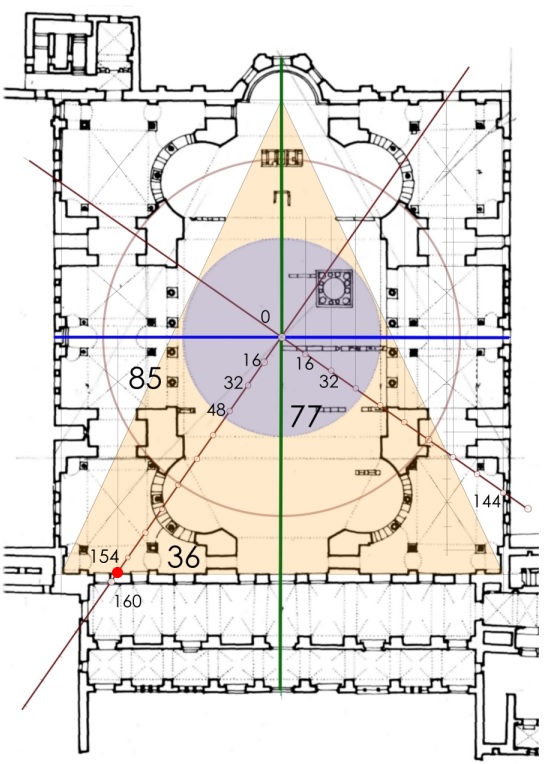
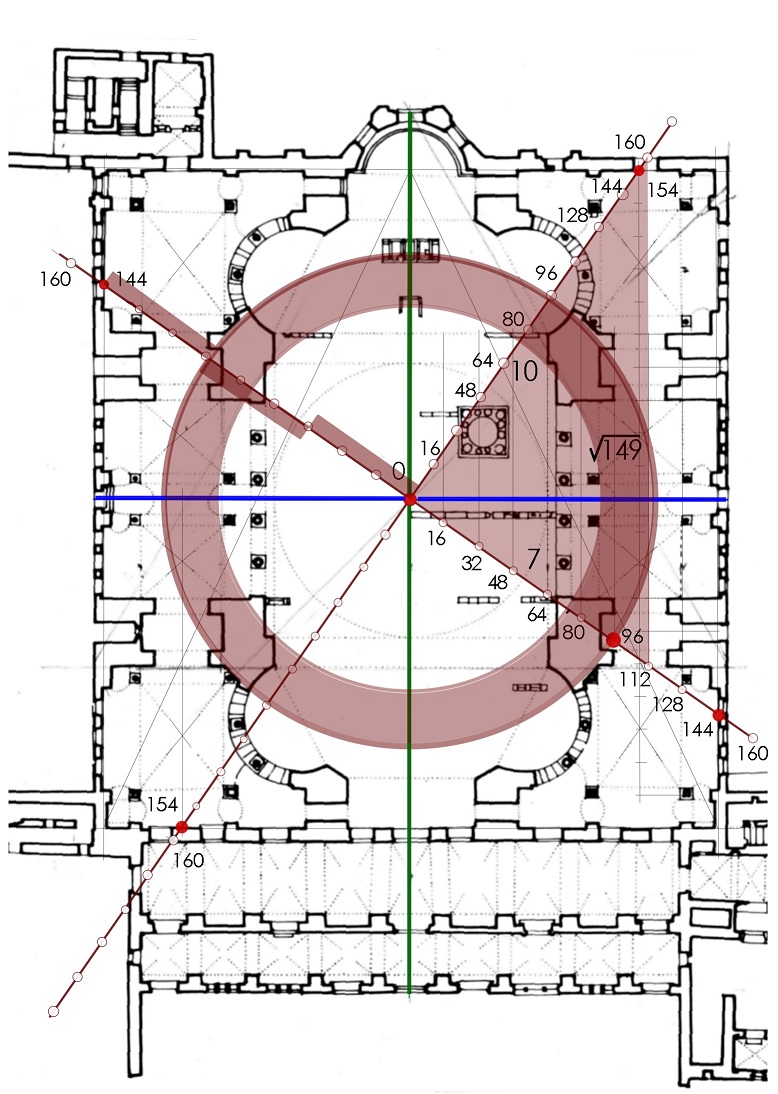
Einmessung, Maße und Zahlen II Das Pythagoreische Dreieck 36-77-85 (Plan HS 2) verdoppelt zu einem gleichschenkligen Dreieck mit der Basis 72 und der Höhe 77, das ganze viermal ergibt die fast quadratische Fläche des Innenraums 288 zu 308. Die Nordrichtung halbiert den größeren Winkel in zwei spitzere mit dem...