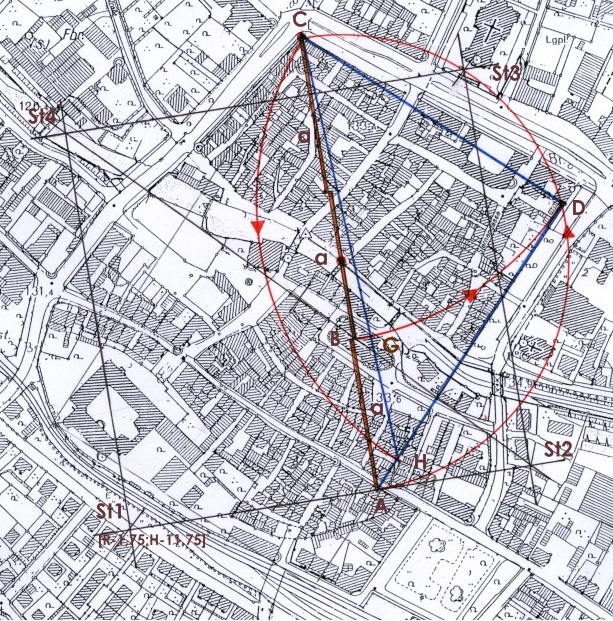
Abb. 11 Eine Katasterkarte der Altstadt mit dem Steinkreuzviertelquadrat St1-St2-St3-St4, über der Teilungslinie A-C die Dreieckskonstruktion über A-C-D.
Über der Strecke A-C liegt nach Osten hin das rechtwinklige Dreieck A-C-D mit den Seitenlängen:
A-C = 3a
C-D = 2a
A-D = a x Wurzel5
In diesem Dreieck liegt das gleichschenklig-rechtwinklige Dreieck C-D-H mit den Seitenlängen:
C-D = 2a
D-H = 2a
C-H = 2a x Wurzel2
C-D ist die Breite der Stadt an ihrer nordöstlichen Seite.
C-H ist die Flucht der Stadtmauer nördlich der Alb.
C-H schneidet die Steinkreuzdiagonale St2-St4 in Punkt G. Über Punkt G steht der Turm von St. Martin.
Die in den Plänen rot gezeichneten Hilfslinien, vor allem die Kreise, sollen geometrische Konstruktionen verständlich machen. Zur Ihrer Absteckung im Maßstab 1:1 ist es nicht nötig, am freien Ende langer Seile sämtliche Bögen und Linien abzulaufen bis die gewünschten Punkte an ihrem Platz sind. Punkt D zum Beispiel, dessen Position zunächst von praktischen Überlegungen bestimmt ist, könnte man grob einmessen und sich dann mit kurzen Bogensegmenten einpendeln, bis man genau den Schnittpunkt hat, der seine Lage definiert.
Ettlingen, Geometrie