17. Grundrechteck

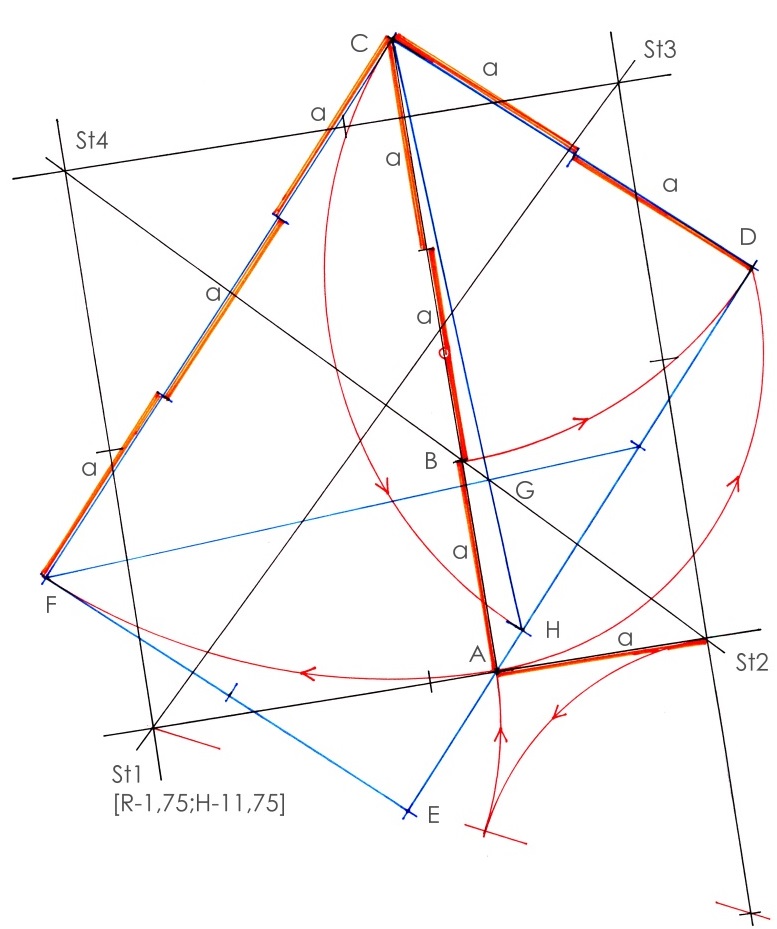
Abb. 22

Gegeben ist das Steinkreuzviertelquadrat St1‑St2‑St3‑St4.

1. Teilung der Strecke St1-St2 nach dem Goldenen Schnitt, Teilpunkt A. Der kleinere Abschnitt „a“ liegt bei St2.
2. Senkrechte auf St1-St2 in A, Länge 3a, Endpunkt C (Lauerturm). Schnittpunkt B (Turmfundament Alt-St.- Martin) mit der Quadratdiagonalen St2-St4, daraus ergibt sich A‑B=a.
3. Konstruktion des Dreiecks A-D-C:
3.1 Halbkreis über A-C.
3.2 Kreis um C mit r=2a, Schnittpunkt mit dem Halbkreis in D.
4. Kreis um D mit r=2a, Schnittpunkt mit der Dreiecksseite A‑D in H.
5. Verlängerung von D-H=2a um die Länge 1a, Endpunkt E, Länge der Strecke D-E=3a.
6. Ergänzung von C-D-E zu dem Rechteck C-D-E-F.

1. Die Punkte A und C und die Strecke „a“ sind nach Lage und Länge im Steinkreuznetz definiert. 2a und 3a sind die Seitenlängen des Rechtecks. Punkt C ist ein Punkt A liegt auf der Seite D‑E. Es ist A‑D=a x Wurzel 5.
2. Punkt G (im Turmbereich der Martinskirche) liegt auf der Steinkreuzdiagonalen. Definiert als Schnittpunkt der beiden Winkelhalbierenden aus den Ecken F und C liegt er auf der Querachse des Grundrechtecks. Seine komplizierte Mehrfachbestimmung ist rechnerisch nachweisbar *^.
3. Punkt C ist der Festpunkt, um den sich das Grundrechteck aus der Steinkreuzrichtung herausdreht. Der Winkel A‑C‑H zwischen der Steinkreuzrichtung und der Winkelhalbierenden des Rechtecks lässt sich berechnen als Differenz zwischen dem Winkel A‑C‑D bei C mit dem Tangens 2 zu , und dem 45°‑Winkel der Winkelhalbierenden bei C. Mit 3,19° ist er nur 0,07° kleiner als der Winkel, mit dem sich die Geometrie der älteren Stadt südlich der Alb von der Richtung des Steinkreuznetzes absetzt.

Ettlingen, Konstruktionen