2.2.3 Geometrie III

Metrik – Rothenburger Fuß

Eine Einmessung in dieser Form wäre praktikabel, kann aber auch anders verlaufen sein. Relativ sicher ist die Vorgehensweise in zwei Phasen:

1. Konstruktion des Quadrats, wobei Richtung und Maße auch direkt metrisch angelegt werden können.
2. Verschieben des Quadrats auf den nordsüdlichen Steinkreuzkoordinaten. Für das Maß der Verschiebung, das auch anders sein könnte, spricht hier unter ande­rem der Turm der Fran­ziska­nerkirche der auf der Dreiecks­seite A‑S steht (vgl. RO3.1.2) .

Der Winkel mit dem Tangens 6 zu 13 temperiert die Dif­ferenz der Winkel mit dem Tan­gens  √2und √3 in ein ganzzahliges Verhältnis, das als Bindeglied zwischen der 12-er und 14-er Metrik des Grund­quadra­tes steht. Die Metrik des Grundquadrates kann also auch als temperierte Geometrie verstanden werden, das heißt, die irrationalen Zahlenverhältnisse, die diese Geometrie hervorbringt, werden zu ganzzahligen Maßverhältnissen abgerundet, mit denen sich genau genug arbeiten lässt.

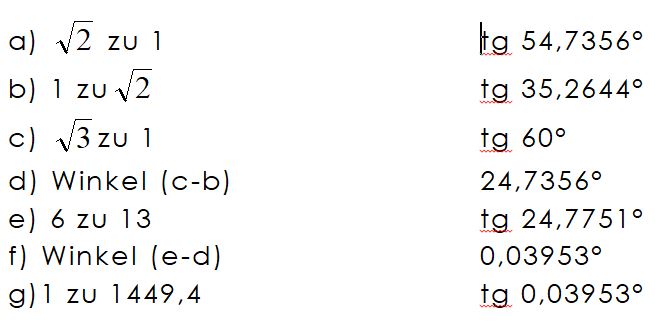
Differenz durch Temperierung
347,635m/1449,4=0,24m

Die Abweichung der Halbdiagonalen H‑C’ aus der Steinkreuzrichtung beträgt:
bei temperiertem Winkel 347,635m/32 =10,86m
geometrisch 347,635m/31,31=11,10m.
Die Strecke H‑C’ sebst wäre 8mm länger.*

Der Rothenburger Fuß, abgeleitet vom Steinkreuzgitter und den Proportionen der Stadtgeometrie **

Für den Rothenburger Fuß wird eine Länge von 0,302m überliefert, 13 Fuß bilden eine Rute. (Quelle: Karl Borchard: Die geistlichen Institutio­nen etc., Neustadt/Aisch 1988)

Aus der Rekonstruktion des Grundquadrates (nach RO 2.1) ergeben sich folgende Maße:

Seitenlänge einer Grund­quadrateinheit       22.22m,
Diagonallänge einer Grundquadrateinheit  31,42m,
auf der Diagonalen 8 Ruten zu 13 Fuß = 104Fuß zu  0,302m.
Berechnung direkt aus halber Steinkrezeinheit E+/2 374,635m/224x√205x√2/8/13=0,302m
Seitenlänge – Diagonale Grundquadrateinheit 22,22mx√2=31,42m

→ WEITERLESEN

ANMERKUNGEN

* Das gleiche Quadrat wie in Rothenburg findet sich auch  in Ulm, allerdings um die Ostwestachse der Stein­kreuzlinien gespiegelt. Dort wurde zur Nordsüdanbindung an die nächste Steinkreuzlinie eine Seite des 12-er Quadrats verdoppelt, eine zweite von 12 auf 2×13 Einheiten verlängert.

** Das ist kein Einzelfall. Auf ähnliche Weise lässt sich auch der Würzburger Schuh aus dem Steinkreuzgitter berechnen.