2.1 Grundquadrat

Zahlen und Maße

Die Einheiten

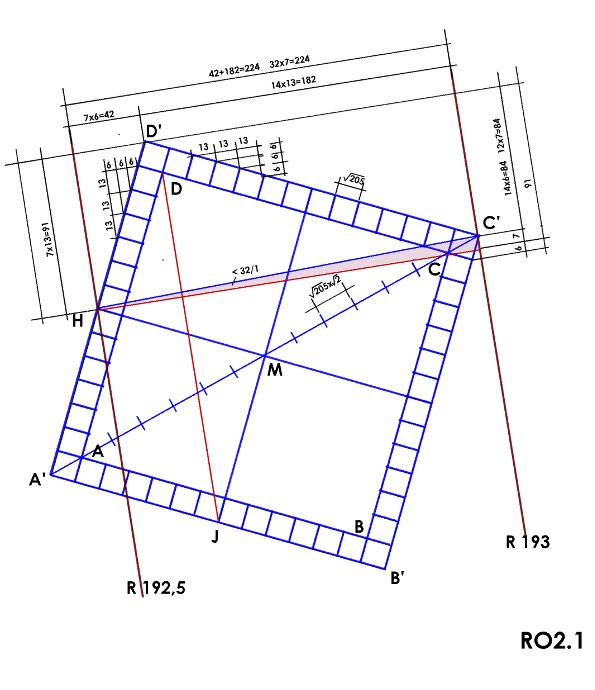
Die Maße des Grund­quadrats lassen sich aus dem Steinkreuznetz geometrisch oder rechnerisch ermitteln über das rechtwinklige Dreieck H‑C’‑D’ mit dem Seitenverhältnis 13 zu 6 zu . An des­sen Katheten liegen 7 bzw. 14 kleinere Dreiecke mit gleichen Seitenverhältnis. Ihre Katheten liegen in Stein­kreuzrichtung. Sie zählen je nach Lage und Richtung 6 oder 13 Einhei­ten, die Hypotenuse zählt  = 14,3178 Einheiten. Sie ist eine der 12 bzw. 14 Einheiten im Grund­quadrat. Bei dieser Konstruktion summieren sich die Dreiecksseiten zwischen der R192,5 und der R193 zu 224 Einheiten: 7×6 von H nach D’ und 14×13 von D’ nach C’. das sind 32×7 Einheiten.

Rechtwinklig dazu ergeben sich 7×13=91 Einheiten von H nach D’ und in Gegenrichtung 14×6=84 Einheiten von D’ nach C’. Bleiben 7 Einheiten Diffe­renz. Um dieses Maß entfernt sich die Halbdiagonale H‑C’ auf eine Länge von 32×7 Einheiten von der Steinkreuzrich­tung. Die Abweichung beträgt danach 1 zu 32.

Der Abstand R192,5 zu R193 misst E+ /2=347,635m. Das ergibt für eine Grundquadrateinheit:

347,635m/224x=22,22m.

Die Seitenlänge des 12-er Quadrats mißt 22,22mx12=266,65m, des 14-er Quadrats 22,22mx14=311,09m.

Koordinaten

Koordinatennullpunkt für die Untersu­chungen ist der Quadradratmittelpunkt M: +‑0Q;+‑0H.

Koordinatenbeispiele:
Punkt A                                   -6Q/ -6H
Punkt B                                     6Q/ -6H
Punkt C’                                   7Q/  7H
Punkt H                                   -6Q/+-0H.

→ WEITERLESEN