1.3 Der Ostrand der Stadt

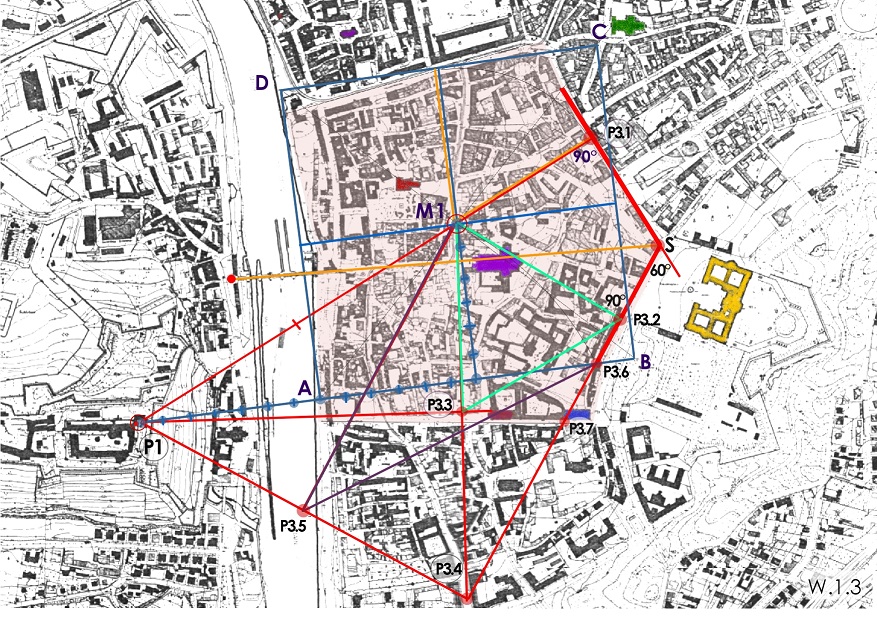
Die nordöstliche Flucht, die Theaterstraße, steht senkrecht auf der Verlängerung der Linie Marienturm – Mitte Grundquadrat (P1-M1). Die Verlängerung M1-P3.1 entspricht einer halben Quadratseite.

Die südöstliche Flucht, Residenzplatz und Balthasar-Neumann-Promenade, knickt – in Punkt S – in einem 60°-Winkel von der nordöstlichen Flucht ab. Senkrechter Abstand zur Quadratmitte ist die halbe Strecke P1-M1. Eingezeichnet ist eine einfache Konstruktion mit dem gleichseitigen Dreieck M1-P3.2-P3.3 (grün).

Die Ost-West-Achse der Stadt : Alte Mainbrücke – Domstraße – Dom zielt auf Punkt S.

Die Geometrie

Der Ausgangspunkt der Vermessung dürfte vor dem Marienturm zu suchen sein, in Punkt P1. Die Flucht von dort zur Mitte M1 des Grundquadrates liegt im Grundquadrat selbst in einem Winkel von 13zu6*.

Die Konstruktion:

1. Über der Strecke P1-M1 nach Südosten das gleichseitige Dreieck P1-M1-P3.4 (rot),
2. eine Senkrechte auf P1-P3.4 in P3.4 zu Punkt S,
3. der Winkel P3.4-P1-P3.6 (rot-blau), tg 1zu 2, konstruiert mit einem Kreis um die Seitenmitte P3.5, Radius die Dreieckshöhe (violett), Schnittpunkt mit der Senkrechten in P3.6, von P1 durch diesen Punkt die Flucht für die Grundquadratseite A-B und ihre Verlängerung A-P1(blau)**.

Damit lassen sich die Umrisse des Stadtgebietes östlich des Mains geometrisch ableiten aus dem gleichseitigen Dreieck P1-P3.4-M1, das seinerseits definiert ist durch eine seiner Seiten, der Fluchtlinie vom Marienturm auf der Festung zum Mittelpunkt des Grundquadrates.

Punkt P3.7 halbiert die Strecke S-P3.4. Hier kreuzt die Achse des Neubau-Straßenraums. Die Achse liegt darin zentral im westlichen Bereich, in der verengten Straße näher an den vorspringenden Kirchenbauten.

Aus historischer Sicht ist die Einmessung dieses Stadtgebietes eine Erweiterung. Offensichtlich ist sie nicht als Anhang konzipiert, sondern als selbstständige Komposition, die fraglos Altes in sich aufzunehmen hatte.

→ WEITERLESEN

ANMERKUNGEN

*)Das Zahlenverhältnis steht hier und im Folgenden für den Tangens (tg) eines Winkels. Der Winkel mit dem Tangens 13zu6 ist in mittelalterlichen Stadtgeometrien häufig nachzuweisen. (Rothenburg oT, Ulm, Worms). Aus der Würzburger Geometrie erklärt sich zugleich auch seine Vorzugsstellung. Hier teilt er sich einen der drei 60°-Winkel im gleichseitigen Dreieck mit einem anderen prominenten Winkel, dessen Tangens das Verhältnis von Quadratseite zur Quadratdiagonalen ist (das bei Halbierungen gleichbleibende Seitenverhältnis der DIN-Papierformate), in Zahlen: 1zu √2 = tg 35,26°, tg(60°-35,26°)=13zu5,989.
Die Temperierung von 13zu5,989 auf 13zu6 ergibt für die 972m lange Strecke P1-P3.6 eine Differenz von 67cm.

** In Zahlen: Dreiecksseite =2, Höhe = √3 =Strecke P3.5-P3.6, ergibt für die Strecke P3.4-P3.6= √2 , verhält sich zu P3.5-P3.4 wie √2 /1.