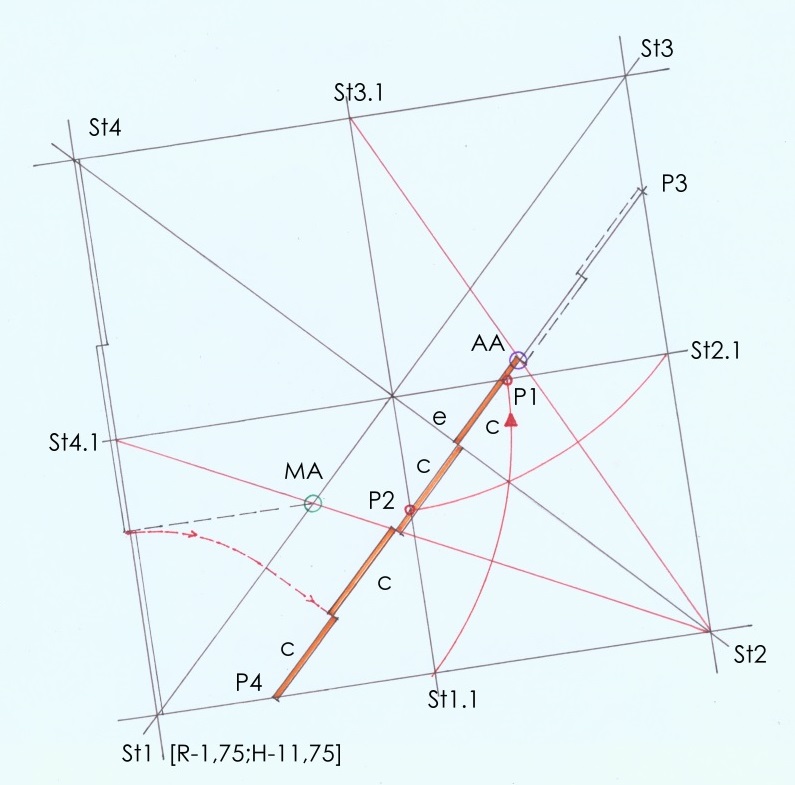
Abb. 23
Gegeben ist das Steinkreuzviertelquadrat St1-St2-St3-St4, Seitenlänge ½ E+ = 347,625m. Eingezeichnet sind die Mittelsenkrechten auf die Quadratseiten und die Diagonalen.
1.1 Kreis um die Seitenmitte St4.1, Radius die Diagonallänge St4.1.-St1.1, Schnitt mit der Mittellinie St4.1-St2.1 in P1.
1.2 Kreis um die Seitenmitte St3.1, Radius die Diagonallänge St3.1-St2.1, Schnitt mit der Mittellinie St1.1-St3.1 in P2.
1.3 Parallele zur Diagonalen durch P1 und P2 bis zu den Quadratseiten.
2.1 Die Halbdiagonalen St2-St4.1 und St2-St3.1 schneiden die Diagonale St1‑St3 und die Parallele P3‑P4 in Drittelspunkten, einer davon ist Punkt AA.
2.2 Punkt AA auf der Parallelen wird die Spitze des Alten Dreiecks.
Sie entsteht durch die Aufteilung der Parallele P3‑P4 in 6 Teilstrecken; rechnerische Länge der Teilstrecken 64,97m.
4.1 MA auf einem Drittelspunkt der Diagonalen wird später Mittelpunkt des Kreises für die drei Türme.
4.2 Interessant im Zusammenhang mit Punkt MA ist eine Alternative Konstruktion von „c“: Kreis um St1 mit 1/3 Seitenlänge St1‑St4 als Radius auf die Diagonale St1‑St3, vom aus Schnittpunkt eine Senkrechte teilt das erste Drittel der Parallelein in zwei Teile mit der Länge „c“.
Abgeleitet von der halben Seitenlänge des Steinkreuzviertelquadrates
¼ E+ = 173,81m
ergeben sich folgende Zahlenverhältnisse und Maße, dabei steht für ¼ E+ die Zahl 1:
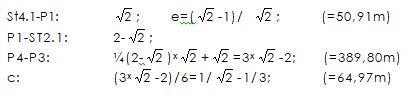
Ettlingen, Konstruktionen