14. Istanbul, Hagia Sophia

Einmessung, Maße und Zahlen II

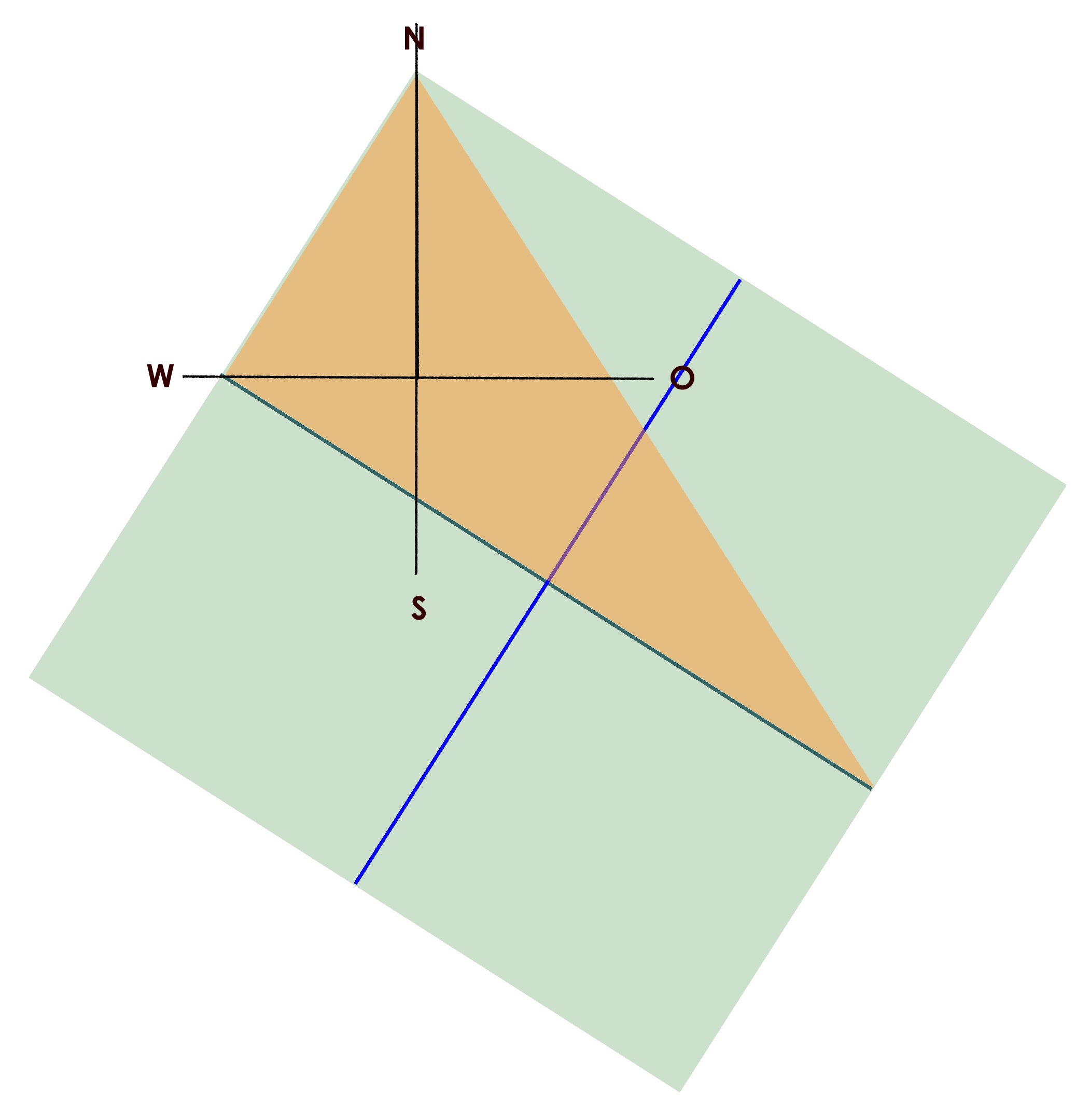
Das Pythagoreische Dreieck 36-77-85 (Plan HS 2) verdoppelt zu einem gleichschenkligen Dreieck mit der Basis 72 und der Höhe 77, das ganze viermal ergibt die fast quadratische Fläche des Innenraums 288 zu 308.

Die Nordrichtung halbiert den größeren Winkel in zwei spitzere mit dem Tangens 7 zu 11, (Plan HS 7)

Bei einer Addition der Winkel 7/11=tg32,47° und 7/10=g34,99° bleibt bis 90° ein Restwinkel von 22,54°, sodass  möglicherweise hier auch auch an ein  8- bzw. 16-Eck mit 22,5°-Winkeln gedacht wurde.

Die schräg zur Längsachse liegende  85 bzw. 170 lange Dreieckseite ist dezimal teilbar in10x17 bzw. 20×8,5 Abschnitte. 17 projiziert auf die Längachse werden zu 15,4 (Plan HS 3).

Ein Bezug zum verwendeten Pythagoreischen Dreieck 15‑8‑17 stellt sich ein: 5×17=85 (Plan HS 4).

Zum Abstand Mitte Haupkuppel zu den Mittelpunkten der Halbkuppeln gibt es mehrere Möglichkeiten zu untersuchen:

A) 7 zu 10 Verschnitte nach Plan HS 4, Abstand 73,4;
A1) Abstand nach Zahl 73,5 =77/11×10,5, Diff.<3cm.
B) 7,07 zu 10 (1/√2) Verschnitte, Abstand 73,9;
B1) Abstand nach Zahl: 74 = Kuppelradius +10 (10=Differenz von Längs- und Querachse ab Mitte).

Die vorliegenden Pläne tendieren graphisch zu A). Maße liegen nicht vor.

Als größere Maßeinheit sind 16M (=3,88m) feststellbar: Innenraumbreite 18×16=288M, Kuppeldurchmesser bzw. Quadratseiten unter der Kuppel 8×16=128M. Außenmaß längs (graphisch) 20×16=320M.

Restflächen um das zentrale Quadrat 128x128M, links und rechts der Hauptache: Entlang der  Nordwest und Südostwand: je  2x 144x90M. An Nordost- und Südwestwand: 2x80x128M. Alle 6 Rechtecke haben das Seitenverhältnis 5 zu 8.

In vielen Fällen handelt es sich um mathematische Eigenläufer. Sie ergeben sich aus  der Geometrie und den Zahlen als Produkt der kompositorischen Qualität.