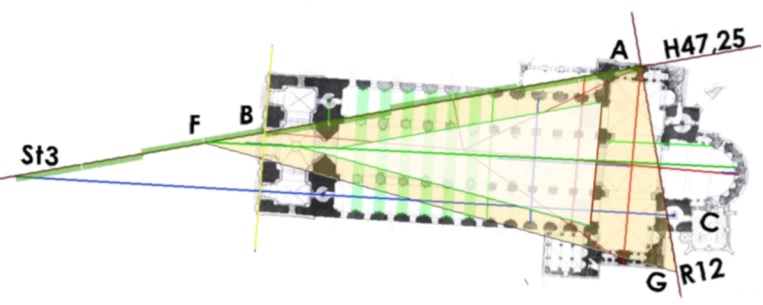
Maße:
A‑B=33 E+/220
A‑F=33+5,5=38,5=77/2 E+/220
A‑C=13 E+/220
A‑G=13+5=18=36/2 E+/220
F‑G=42,5=85/2 E+/220
A‑St3=55 E+/220=173,82m
Im Winkel der Steinkreuzlinie R12 und der Koordinate H47,25 liegt das rechtwinklige Dreieck A‑F‑G mit einer weiteren Achse des Doms (grün): der Winkelhalbierenden bei Punkt F. Die Abweichung von der (blauen) Mittelachse ist gering, von der Chorachse erkennbar größer. Bezogen auf die grüne Achse liegt die südliche Dreieckseite spiegelbildlich zur Steinkreuzkoordinaten H47,25. Sie streift die Innenecke der Leibung des romanischen Westportals, eine Parallele dazu von der Südostecke des südlichen Seitenschiffs streift die Leibung des Portals zwischen Vorhalle und Kirchenschiff.
Eine Parallele zur nördlichen Dreieckseite lauft vom Schnittpunkt der grünen Achse mit der inneren Flucht der Westwand des Kirchenschiffs zur Nordostecke des nördlichen Seitenschiffs.*
A‑F‑G ist ein Pythagoreisches Dreieck mit dem Seitenverhältnis 36/77/85.** Die Maßeinheit ist E+ /220/2=1,58m. Die von der Spitze F ausgehenden Seiten weichen von der grünen Achse im Verhältnis 9 zu 2 ab.
Die ersten sechs Pfeilerpaare des Kirchenschiffs stehen – in ungleichen Abständen – innerhalb von Feldern, die abwechselnd leer und besetzt sind. Sie sind senkrecht zur grünen Achse gleichmäßig auf den beiden Dreiecksseiten eingemessen mit E+ /220=3,16m. Daraus ergibt sich auf der grünen Achse eine Feldbreite ist von 3,085 und ein durchschnittlicher theoretischer Achsabstand der Pfeiler von 6,17m.
* Vergleichbar im Ulmer Münster eine Parallele zu westöstlichen Stadtachse von der Turmmitte im Vorraum zur Nordostecke des Mittelschiffs mit dem Sakramentshaus.
** Vgl. Istanbul, Hagia Sophia: Die Hauptachse des Innenraums wird von den 77‑er Seite zweier aneinander liegender 36/77/85 –Dreiecke gebildet. Die Querachse mißt 2×36 Einheiten. Die Winkelhalbierende eines Dreiecks ist genordet.
Speyer/Karlsruhe