Geometrischer Nachweis ohne Rechenoperationen.
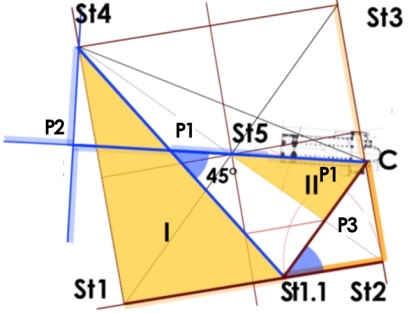
1. Der halbe rechte Winkel
Dreieck [I] liegt an einer Seite, Dreieck [II] an einer Diagonalen des Quadrats St1‑St2‑St3‑St4, also um 45° gegeneinander verdreht.
Die beiden Dreiecke [I] und [II] sind rechtwinklig und ähnlich.
Das Kathetenverhältnis des größeren Dreiecks [I] ist nach dem Goldenen Schnitt konstruiert. Die Diagonale St2‑St5 wird durch St1.1‑C ebenfalls nach dem Goldenen Schnitt geteilt. Die größere Teilstrecke ist die Kathete St5‑P3, die kleinere Kathete P3‑C ist gleich der kleineren Teilstrecke P3‑St2.
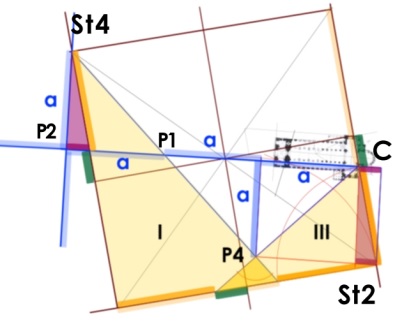
2. Die Strecke „a“
Die Dreiecke [I] und [III] sind rechtwinklig und ähnlich. Sie überschneiden sich im rechten Winkel. P4 ist der Schnittpunkt ihrer Hypotenusen. Eine senkrechte von P4 auf C‑P1 bildet zwei gleichschenklige rechtwinklige Dreiecke mit der Schenkellänge a., die deckungsgleich sind mit dem Dreieck P1‑P2‑St4.
(Die Achse C‑P2 läuft durch die Quadratmitte und schneidet die beiden Quadratseiten jeweils in gleichem Abstand (grün). Die Strecke St2‑C hat die Länge a. Die Strecke P2‑St4 ist so lang wie die Strecke St2‑C und damit ebenso lang wie a.)
Speyer/Karlsruhe